At work I've been using gnuplot to do some function-fitting for me. In the course of that I came across a page on computing basic statistics with gnuplot, and it got me to thinking about how to apply this to something meaningful — you know, like baseball.
Note: I'm not an expert in statistics. I haven't ever taken a statistics course. If I get something wrong, please correct me gently. Thank you.
That said, it's been often remarked that On-Base percentage (OBP), Slugging Percentage (SLG), and their offspring, On Base Plus Slugging (OBP) are more highly correlated with runs scored than the traditional batting average (AVG). But how do we quantify that? With statistical analysis, of course.
We need data. I went to Major League Baseball's team statistics database and pulled off the AVG, OBP, SLG, OPS, and Runs/Game data from 1996 through 2011. That gave me data for 476 team/seasons, all playing 161, 162, or 163 games. That should be enough data for a start.
First let's look at the relationship between batting average and runs per game. We'll go through this on in reasonable detail. The data top of the datafile, which we'll call runs.dat, looks like this:
# AVG OPB SLG OPS RPG
0.293 0.369 0.475 0.844 5.913
0.288 0.360 0.436 0.796 5.377
0.288 0.357 0.425 0.782 5.414
0.287 0.355 0.472 0.827 5.932
0.287 0.366 0.484 0.850 6.168
0.284 0.358 0.469 0.827 5.693
0.283 0.359 0.457 0.816 5.728
0.281 0.360 0.447 0.807 5.543
0.279 0.353 0.441 0.794 5.519
The full file is available on request.
Plot out runs per game versus average:
set title "Correlation of Runs with Batting Average"
set format x "%.3f"
set format y "%.1f"
set xlabel "AVG"
set ylabel "Runs/Game"
plot "runs.dat" using 1:5 notitle w p lt 1 pt 7 ps 1
which looks like this:

OK. As we might expect, there is some correlation. Runs go up as the batting average improves. How much? We can use gnuplot's fitting routine to see. We'll assume a straight-line fit:
linear(start,slope,x) = start + slope*x
fit linear(avgstart,avgslope,x) "runs.dat" using 1:5 via avgstart,avgslope
set key left reverse Left
print avgstart, avgslope
replot avgstart + avgslope*x t "Linear Fit" w l lt 3 lw 2
Which produces a couple of numbers:
-5.07322075997934 37.0579378737095
and the plot

The slope of the line is 37.06, which tells us that a change in batting average from 0.260 to 0.270 will add another 0.37 runs per game to a teams scoring (on average). (Note that the fit misbehaves if we get a low batting average, predicting a negative number of runs. That's because this isn't a great model for baseball at all levels. We're only considering Major League Baseball, where most batters are able to at least make contact with major league pitching, and so can be expected to hit above 0.200 the Mendoza Line. Don't worry about that for now, we'll look for better fits later on in this series, if it should continue.)
How good is this fit? One way to quantify a fit is by the sample correlation coefficient, which in our case can be written as
R = <(x - <x>)(y - <y>)>/[σ(x) σ(y)] ,
Where x is the data on the x-coordinate of the plot (here AVG), y the data along the y-axis (here Runs/Game), and the brackets mean take the average
. Careful authors don't call σ the standard deviation, but I will:
σ(x) = <(x - <x>)2>½ ~ .
The theory of R is simple. If R = 1, then all of the data in the last plot would fall on the line, and the line would slope upward. Then AVG and RPG would be perfectly correlated. On the other hand, if all the data fell on the line, but the line sloped downward, than R = -1, and AVG and RPG are prefectly anti-correlated. And if R = 0, there would be no correlation either way. So the closer |R| is to 1, the better AVG and RPG are correlated. (Standard disclaimers apply.) If R = 1 in the above plot we'd be able to perfectly predict how many runs a team would score if we just knew the team batting average. So what is R here?
To find R we'll need to find a lot of averages. Fortunately gnuplot is up to it. Suppose we wanted to fit the data in the last plot to a horizontal line. The formula for that is just f(x) = constant, and constant
would just be the average value of the y (RPG) data. We can do the same thing with a vertical line for x. So to get the averages for AVG and RPG we write
fit linear(avgba,0.0,x) "runs.dat" using (1.0):1 via avgba
fit linear(avgrpg,0.0,x) "runs.dat" using (1.0):5 via avgrpg
print avgba, avgrpg
The (1.0) in the fit routine tells gnuplot that the x-variable is a constant equal to 1. Actually it's a dummy. We don't care what x is, but we have to tell gnuplot something. The :1
or :5
tell gnuplot to get the y axis data (the functional values) from the first or fifth columns.
Which gives us output:
0.264920168067234 4.74417436974786
We can judge the reasonableness of this with a little addition to the plot:
set arrow 1 from avgba,graph 0 to avgba,graph 1 nohead lt 2
set arrow 2 from 0.230,avgrpg to 0.300,avgrpg nohead lt 2
set label 1 "<AVG>" at avgba+0.001,graph 0.1 left
set label 2 "<RUN>" at 0.232,avgrpg+0.1 left
replot
(Using graph 0
on the x-coordinate has never worked for me in gnuplot.)
Which gives us a plot that looks like this:

The standard deviations work similarly, we're just averaging things in one dimension again:
fit linear (sigavg2,0.0,x) "runs.dat" using (1.0):(($1-avgba)**2) via sigavg2
sigavg = sqrt(sigavg2)
fit linear (sigrpg2,0.0,x) "runs.dat" using (1.0):(($5-avgrpg)**2) via sigrpg2
sigrpg = sqrt(sigrpg2)
print sigavg, sigrpg
set arrow 3 from avgba-sigavg,graph 0 to avgba-sigavg,graph 1 nohead lt 2
set arrow 4 from avgba+sigavg,graph 0 to avgba+sigavg,graph 1 nohead lt 2
set arrow 5 from 0.230,avgrpg-sigrpg to 0.300,avgrpg-sigrpg nohead lt 2
set arrow 6 from 0.230,avgrpg+sigrpg to 0.300,avgrpg+sigrpg nohead lt 2
set label 3 "<AVG>-SIGX" at avgba-sigavg-.001,graph 0.10 right
set label 4 "<AVG>+SIGX" at avgba+sigavg+.001,graph 0.10 left
set label 5 "<RUN>-SIGY" at 0.298,avgrpg-sigrpg+.1 right
set label 6 "<RUN>+SIGY" at 0.232,avgrpg+sigrpg+.1 left
The $1
and $5
in the above tell gnuplot you want to use the data from column 1 and column 5 in mathematical formulas. If we just used 1 or 5 here, gnuplot would interpret them as numbers.
All that done, here's a busy plot with the standard deviations marked off:

Finally, getting <(x - <x>)(y - <y>)> is a little trickier, since it's a fit to two variables. Fortunately, gnuplot can do that. The only trick is that we have to supply four parameters for a two-dimensional fit. The forth column is an error estimate, which we'll take to be one. Note that we have to also define a new functional.
avg2d(const,x,y) = const
fit avg2d(corxy,x,y) "./runs.dat" using (1.0):(1.0):(($1-avgba)*($5-avgrpg)):(1.0) via corxy
print corxy
Now we can compute the r factor, and print it onto the graph:
rfac = corxy/(sigavg*sigrpg)
print rfac
set label gprintf("R = %6.3f", rfac) at graph 0.9,graph 0.2 right
And here's the final plot, which shows that the correlation factor is 0.814. Good, but not perfect:

Here's the entire script in one place, just to make it easier for me to cut and paste, and to annotate it:
set title "Correlation of Runs with Batting Average"
set format x "%.3f"
set format y "%.1f"
set xlabel "AVG"
set ylabel "Runs/Game"
# AVG in column 1, Run/Game in column 5
plot "runs.dat" using 1:5 notitle w p lt 1 pt 7 ps 1
# Our basic linear function
linear(start,slope,x) = start + slope*x
# Find the best linear relationship between AVG and RPG
fit linear(avgstart,avgslope,x) "runs.dat" using 1:5 via avgstart,avgslope
set key left reverse Left
# Plot the fit
replot avgstart + avgslope*x t "Linear Fit" w l lt 3 lw 2
# Get average of batting averages
fit linear(avgba,0.0,x) "runs.dat" using (1.0):1 via avgba
# Get average of runs per game
fit linear(avgrpg,0.0,x) "runs.dat" using (1.0):5 via avgrpg
# Plot some arrows
set arrow 1 from avgba,graph 0 to avgba,graph 1 nohead lt 2
set arrow 2 from 0.230,avgrpg to 0.300,avgrpg nohead lt 2
# And labels
set label 1 "<AVG>" at avgba+0.001,graph 0.1 left
set label 2 "<RUN>" at 0.232,avgrpg+0.1 left
# Now get the standard deviations of AVG and RPG:
fit linear (sigavg2,0.0,x) "runs.dat" using (1.0):(($1-avgba)**2) via sigavg2
sigavg = sqrt(sigavg2)
fit linear (sigrpg2,0.0,x) "runs.dat" using (1.0):(($5-avgrpg)**2) via sigrpg2
sigrpg = sqrt(sigrpg2)
# More arrows:
set arrow 3 from avgba-sigavg,graph 0 to avgba-sigavg,graph 1 nohead lt 2
set arrow 4 from avgba+sigavg,graph 0 to avgba+sigavg,graph 1 nohead lt 2
set arrow 5 from 0.230,avgrpg-sigrpg to 0.300,avgrpg-sigrpg nohead lt 2
set arrow 6 from 0.230,avgrpg+sigrpg to 0.300,avgrpg+sigrpg nohead lt 2
# And labels:
set label 3 "<AVG>-SIGX" at avgba-sigavg-.001,graph 0.10 right
set label 4 "<AVG>+SIGX" at avgba+sigavg+.001,graph 0.10 left
set label 5 "<RUN>-SIGY" at 0.298,avgrpg-sigrpg+.1 right
set label 6 "<RUN>+SIGY" at 0.232,avgrpg+sigrpg+.1 left
# Finally, find the correlation coefficient. Note the 4-component
# call to the fit routine.
avg2d(const,x,y) = const
fit avg2d(corxy,x,y) "./runs.dat" using (1.0):(1.0):(($1-avgba)*($5-avgrpg)):(1.0) via corxy
rfac = corxy/(sigavg*sigrpg)
set label gprintf("R = %6.3f", rfac) at graph 0.9,graph 0.2 right
# And print out the numbers for posterity:
print avgstart, avgslope
print avgba, avgrpg
print sigavg, sigrpg
print corxy
print rfac
replot
And now for the heart of the matter. Let's use the same procedure to look at the correlation between On-Base Percentage and Runs:

R = 0.903, somewhat higher than the AVG/RPG correlation.
How about pure slugging:
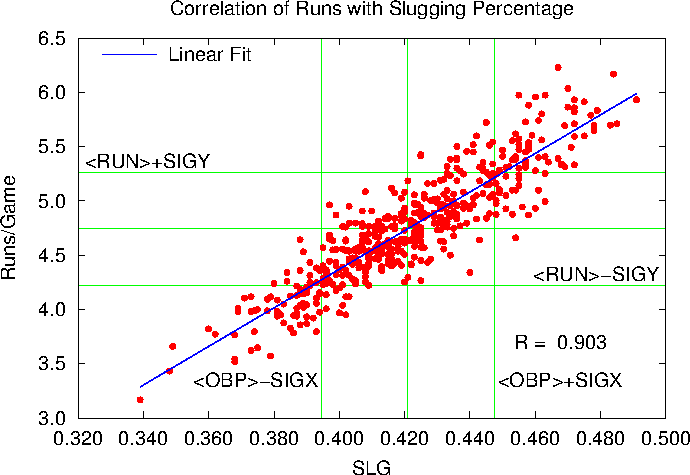
Here R = 0.9026, where above R = 0.9031. OBS and SLG correlate equally well with Runs per game.
So what about everybody's favorite one-number way to evaluate a player?

Here R = 0.952. So our conclusion is that OPS is very well coordinated with Runs scored per game. Better than OBP or SLG, and far better than the batting average.
Now we could do all of this with fancy statistical packages, but for simple stuff like this we can do it all with gnuplot and see everything graphically.
Now that's the story for a very simple set of statistics. What about something like Runs Created? Is it really correlated with Runs per Game? Next time …

















